Deep Learning from Scratch Chapter3 정리

상세한 파이썬 코드는 생략하였음.

Chapter3 word2vec

이번 장에서는 통계 기반 기법 보다 더 강력한 기법인 추론 기반 기법 을 살펴본다.

3.1 추론 기반 기법과 신경

이번 절에서는 통계 기반 기법의 문제를 지적하고, 그 대안인 추론 기반 기법의 이점을 거시적 관점에서 설명한다.

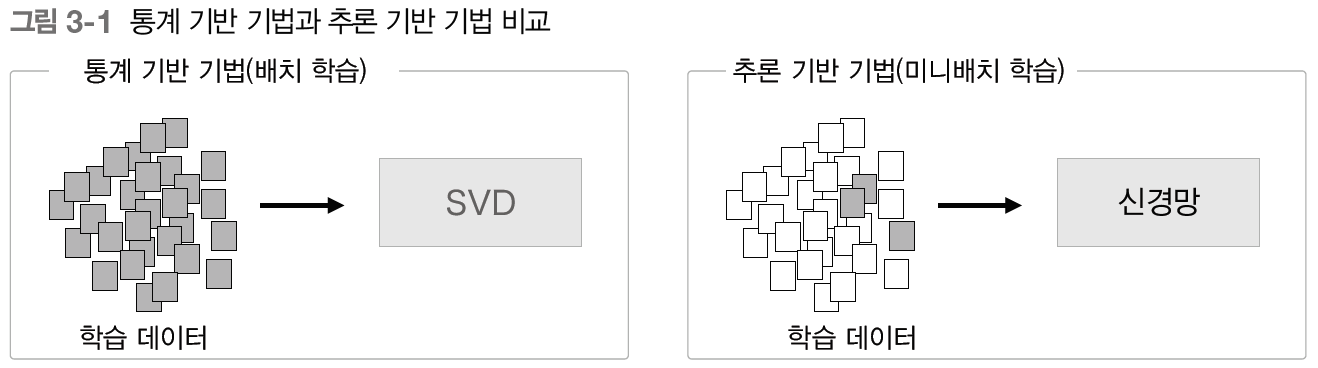
3.1.1 통계 기반 기법의 문제점

통계 기반 기법은 대규모 말뭉치를 다룰 때 문제가 발생한다. 만약 어휘가 100만 개 라면, 100만*100만 이라는 거대한 행렬을 만들게 되고, 이런 거대 행렬에 SVD를 적용하는 것은 굉장히 오랜 시간이 걸리기 때문에 현실적이지 못하다.

한편 , 추론 기반 기법에서는 신경망을 이용하기 때문에 미니배치를 사용하면서 가중치를 갱신한다. 데이터를 작게 나누어 학습(미니배치)하기 때문에 대규모 말뭉치때문에 계산량이 큰 작업을 처리하기 어려운경우에도 신경망을 학습시킬 수 있다.

3.1.2 추론 기반 기법 개요

추론이란 주변 단어(맥락)가 주어졌을 때 무슨 단어가 들어가는지 추측하는 작업을 말한다.

이러한 추론 문제를 반복해서 풀면서 단어의 출현 패턴을 학습하는 것이다.

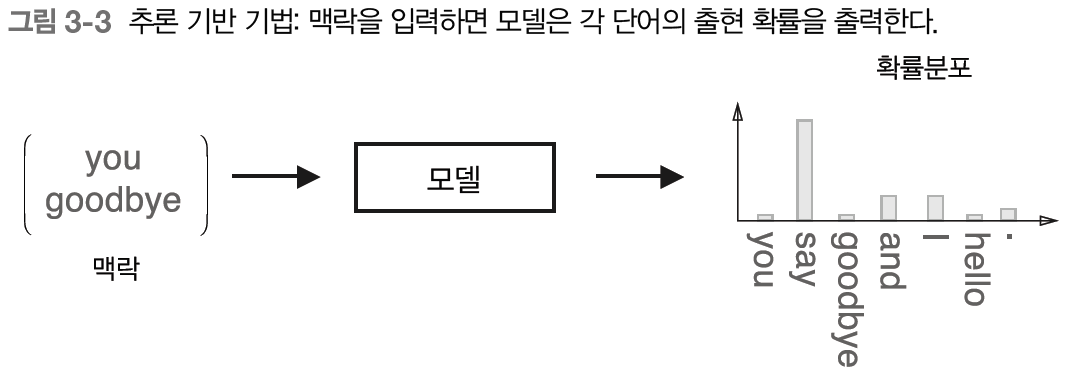
모델은 맥락 정보를 입력받아 출현할 수 있는 각 단어의 출현 확률을 출력한다. 이러한 틀 안에서 말뭉치를 사용해 모델이 올바른 추측을 내놓을 수 있도록 학습시킨다.

3.1.3 신경망에서의 단어 처리

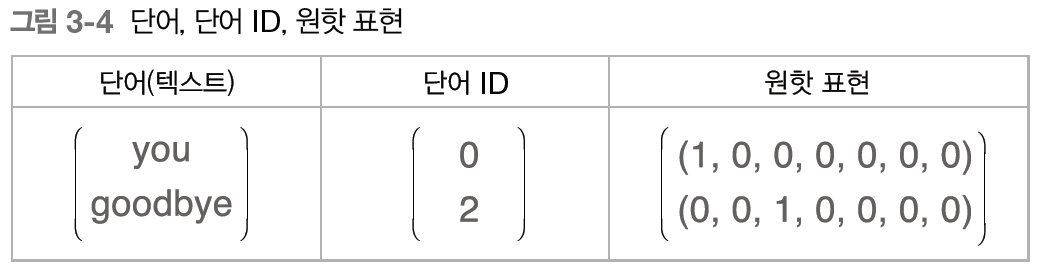
신경망은 단어를 있는 그대로 처리할 수 없으니 원 핫 벡터로 변환한다. 원 핫 벡터는 벡터의 원소 중 하나만 1이고 나머지는 모두 0인 벡터를 말한다.

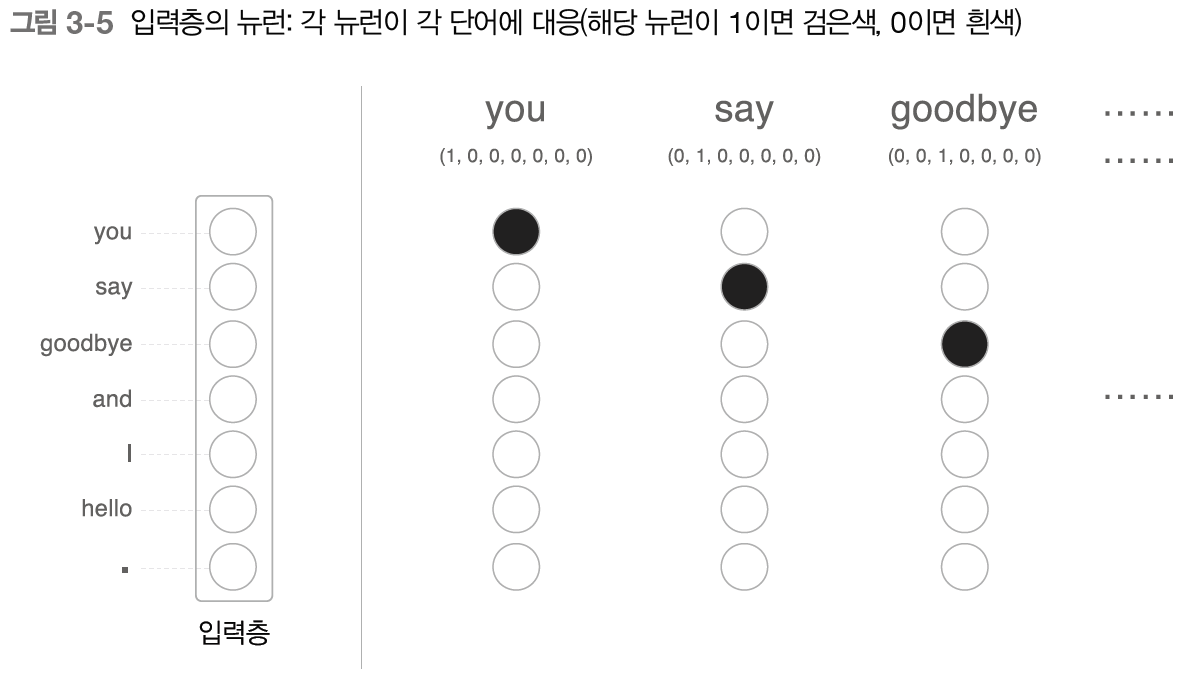
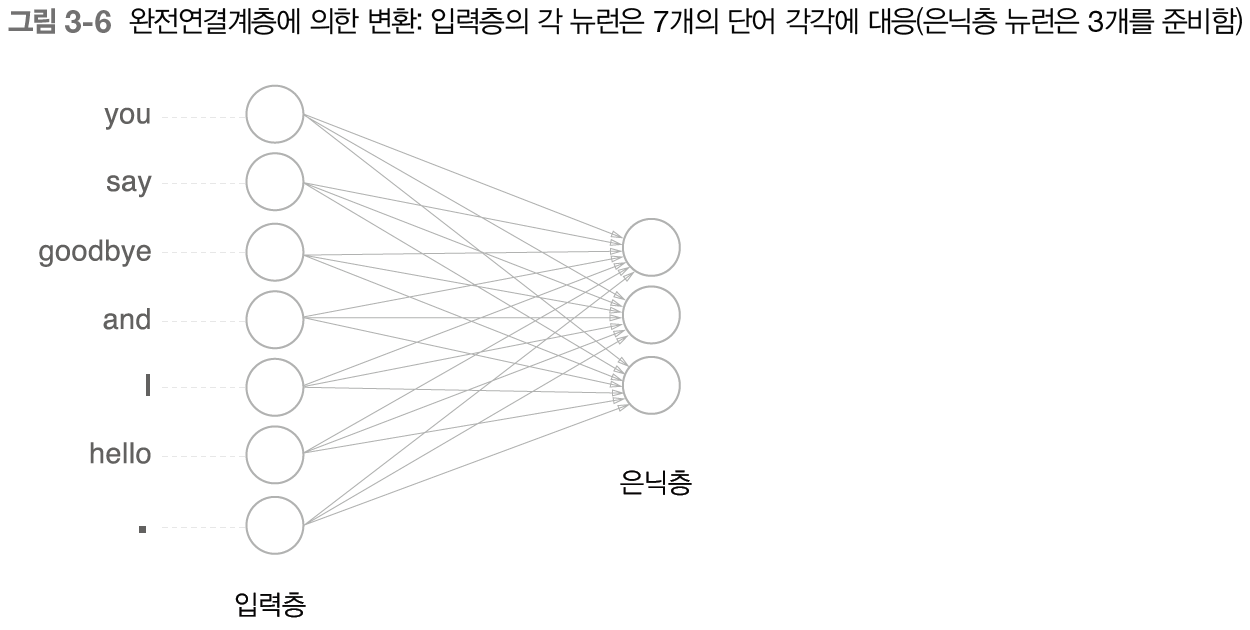
[그림 3-6] 의 신경망은 완전연결계층(Dense Layer)이므로 각각의 노드가 이웃 층의 모든 노드와 화살표로 연결되어 있다.

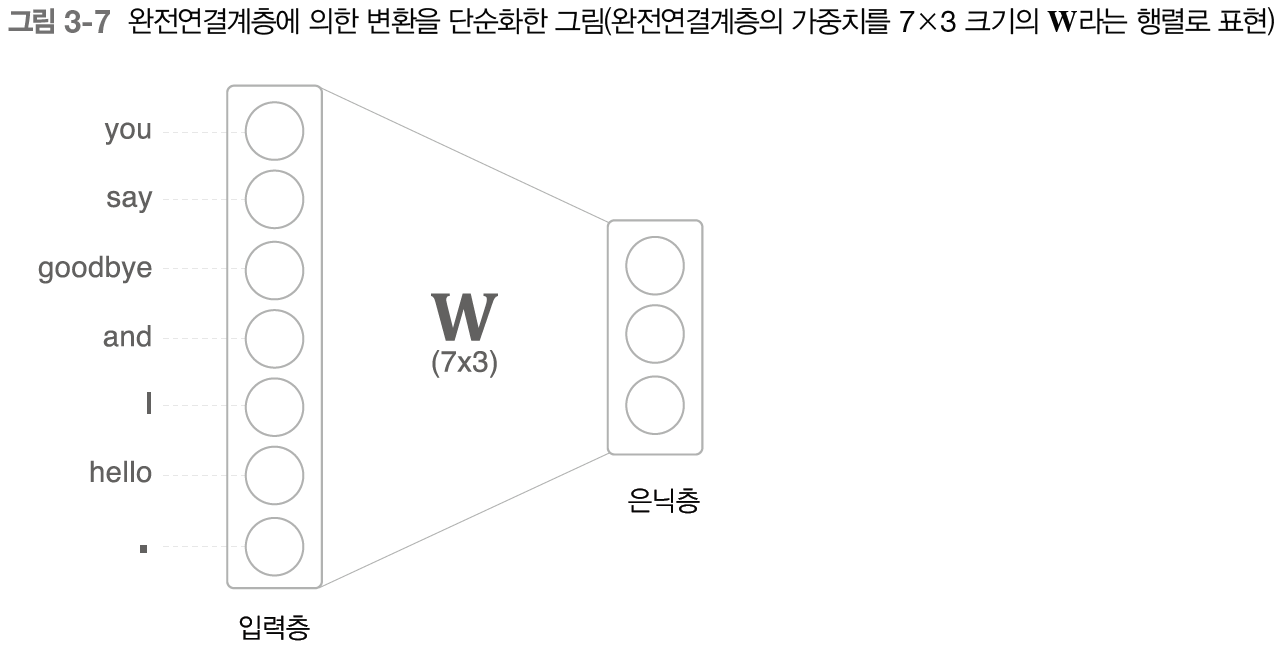
완전연결계층의 계산은 행렬 곱으로 수행할 수 있다(편항 생략).

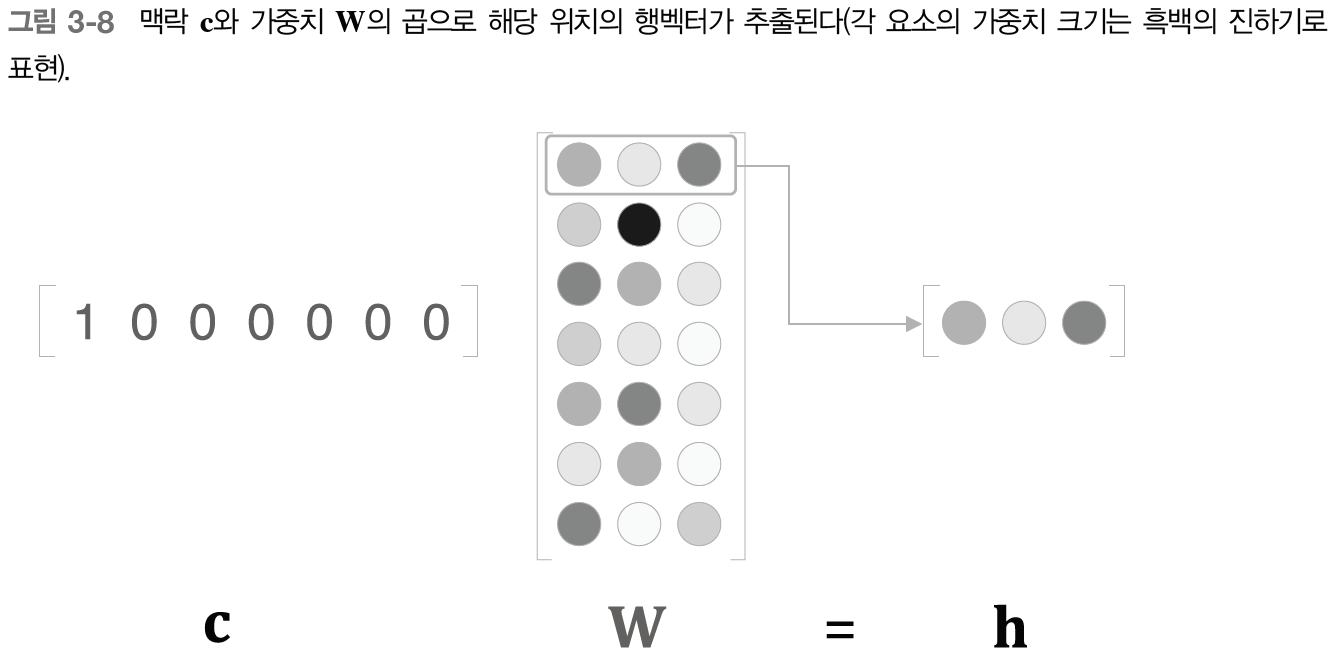
입력 벡터와 가중치 행렬의 행렬 곱에 주목해 보면 입력 벡터는 원 핫 벡터로 단어 ID에 대응하는 원소만 1이고 나머지 원소는 모두 0인 벡터이다. 따라서 입력 벡터와 가중치 행렬의 행렬 곱은 가중치 행렬의 행벡터 하나를 뽑아낸 것과 같다.

3.2 단순한 word2vec

이번 절에서 사용할 신경망 모델은 CBOW(Continuous bag-of-words) 모델이다.

3.2.1 CBOW 모델의 추론 처리

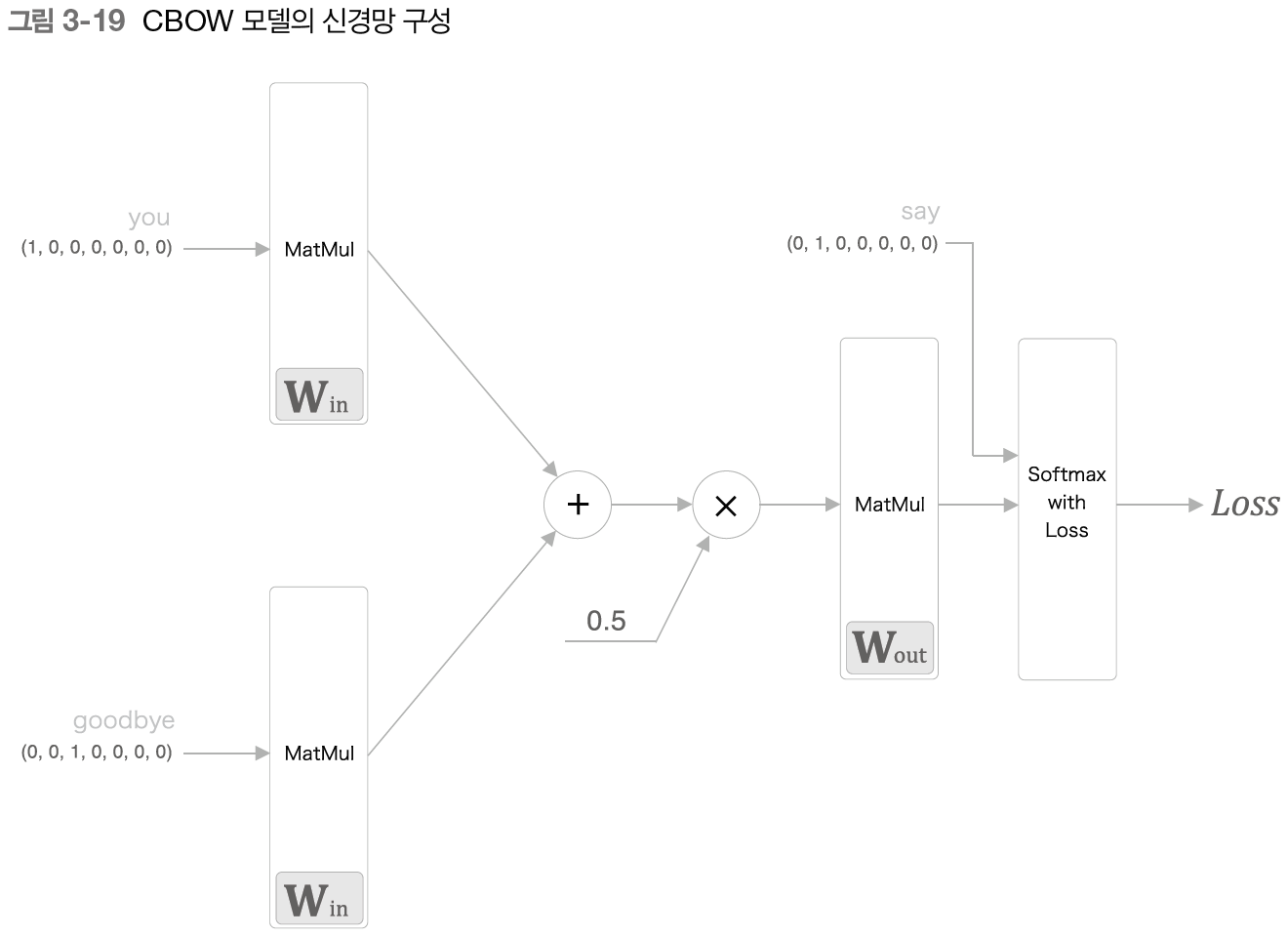
CBOW 모델은 맥락으로부터 타겟을 추측하는 용도의 신경망으로 맥락을 입력으로 받는다.

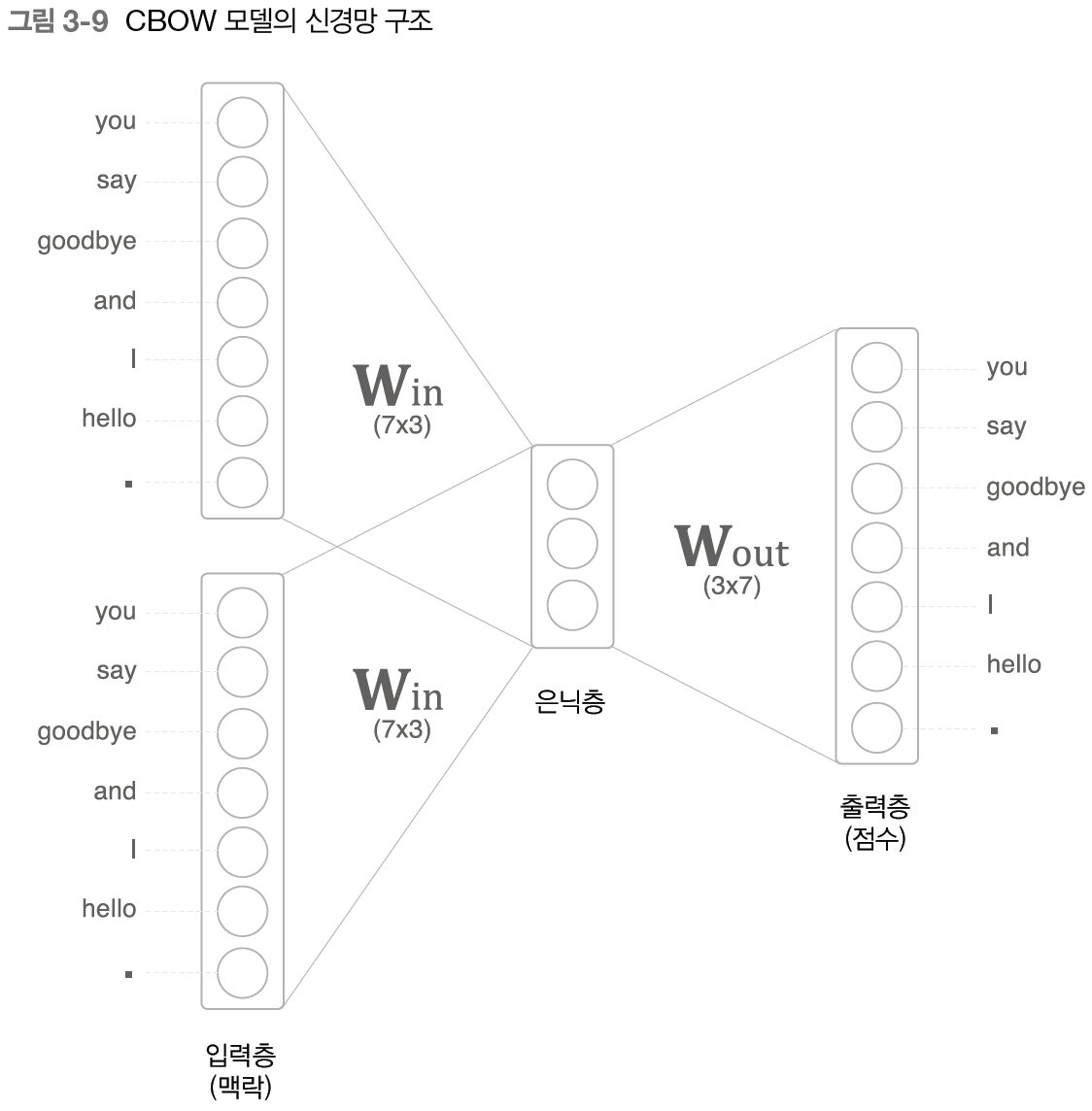
이 모델의 독특한 점은 입력층이 두 개 라는 것이다. 입력층이 두 개인 이유는 맥락으로 고려할 단어를 두 개로 정해기 때문이다. 즉, 맥락으로 고려할 단어가 N개라면 입력층도 N개가 된다.

은닉층의 뉴런은 입력층의 완전연결계층에 의해 변환된 값이 되는데, 입력층이 여러 개이면 입력층 전체를 평균하면 된다.

출력층의 뉴런은 뉴런 하나하나가 각각의 단어에 대응하며 소프트맥스 함수를 적용해 각 단어의 출현 확률을 계산할 수 있다.

은닉층의 뉴런 수를 입력층의 뉴런 수보다 적게 하는 것은 단어 예측에 필요한 정보를 간결하게 담을 수 있으며, 결과적으로 밀집 벡터를 얻을 수 있다.

3.2.2 word2vec의 가중치와 분산 표현

입력층 가중치 $W_{in}$ 의 각 행이 각 단어의 분산 표현에 해당된다. 또한 출력층 가중치 $W_{out}$ 에도 단어의 의미가 인코딩된 벡터가 저장되고 있다고 생각할 수 있다. 다만, 출력층 가중치는 각 단어의 분산 표현이 열 방향(수직 방향)으로 저장된다. 최종적으로 이용하는 단어의 분산 표현으로 어느 쪽 가중치를 사용해야 할 지 선택해야하는데 word2vec에선 입력층 가중치를 대중적으로 사용한다.

3.3 학습 데이터 준비

이번에도 “You say goodbye and I say hello.” 라는 문장을 말뭉치로 사용한다.

3.3.1 맥락과 타겟

다음과 같이 맥락과 타겟을 구현한다. 말뭉치 안의 양 끝 단어를 제외한 모든 단어에 대해 수행한다.

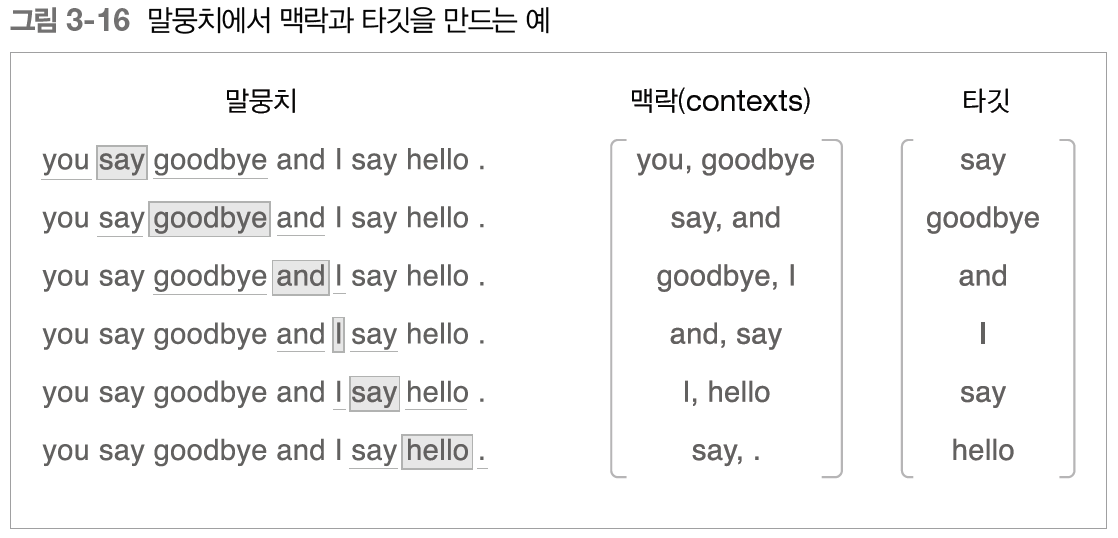
우선 말뭉치 텍스트를 단어 ID로 변환한다.

text = "You say goodbye and I say hello."
corpus, word_to_id, id_to_word = preprocess(text)

다음으로, 단어 ID의 배열인 corpus로부터 맥락과 타깃을 만들어낸다.

contexts, target = create_contexts_target(corpus, window_size=1)

3.3.2 원 핫 벡터로 변환

다음 과정을 통해 맥락과 타켓을 원 핫 벡터로 변환한다.

vocab_size = len(word_to_id)
target = convert_one_hot(target, vocab_size)
contexts = convert_ont_hot(contexts, vocab_size)

3.4 CBOW 모델 구현

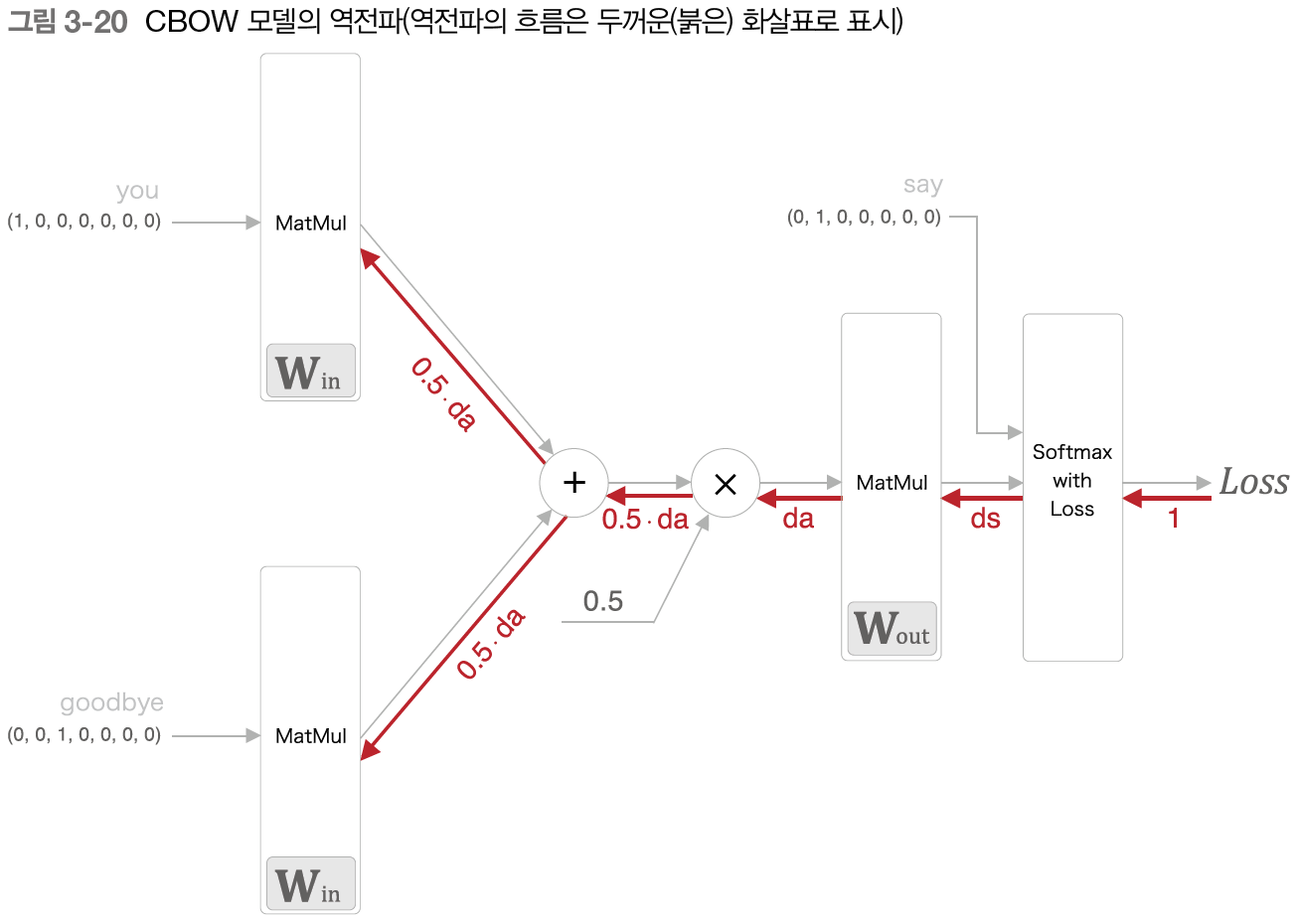
아래와 같은 신경망을 구성한다. 파이토치를 이용해 모델을 구현한다. 자세한 코드는 포스트 맨 마지막에 작성.

3.5 word2vec 보충

3.5.1 CBOW 모델과 확률

맥락으로 $w_{t-1}$과 $w_{t+1}$이 주어졌을 때 타겟이 $w_{t}$가 될 확률을 수식으로 표현하면 다음과 같다.

\[P(w_{t}|w_{t-1},w_{t+1})\]

위 수식을 이용해 크로스 엔트로피 오차 함수를 활용한 CBOW 모델의 손실 함수도 간결하게 표현할 수 있다.

\[L=-logP(w_{t}|w_{t-1},w_{t+1})\]

이를 음의 로그 가능도(Negative log likelihood) 라고 한다. 위 수식은 샘플 데이터 하나에 대한 손실 함수로, 이를 말뭉치 전체로 확장하면 다음 식이 된다.

\[L=-\frac{1}{T}\sum^T_{t=1}\log{P(w_{t}|w_{t-1},w_{t+1})}\]

위 수식은 윈도우 크기가 1인 경우만 작성하였지만, 다른 크기(m개)라도 해도 수식으로 쉽게 나타낼 수 있다.

3.5.2 skip-gram 모델

skip-gram 모델은 CBOW에서 다루는 맥락과 타겟을 역전시킨 모델이다.

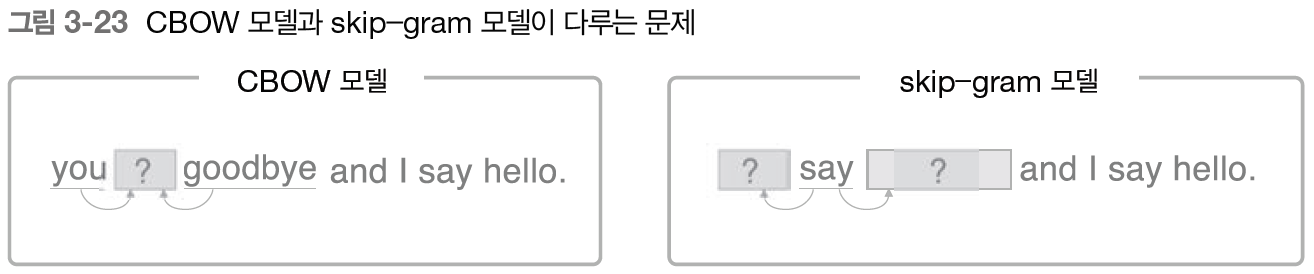
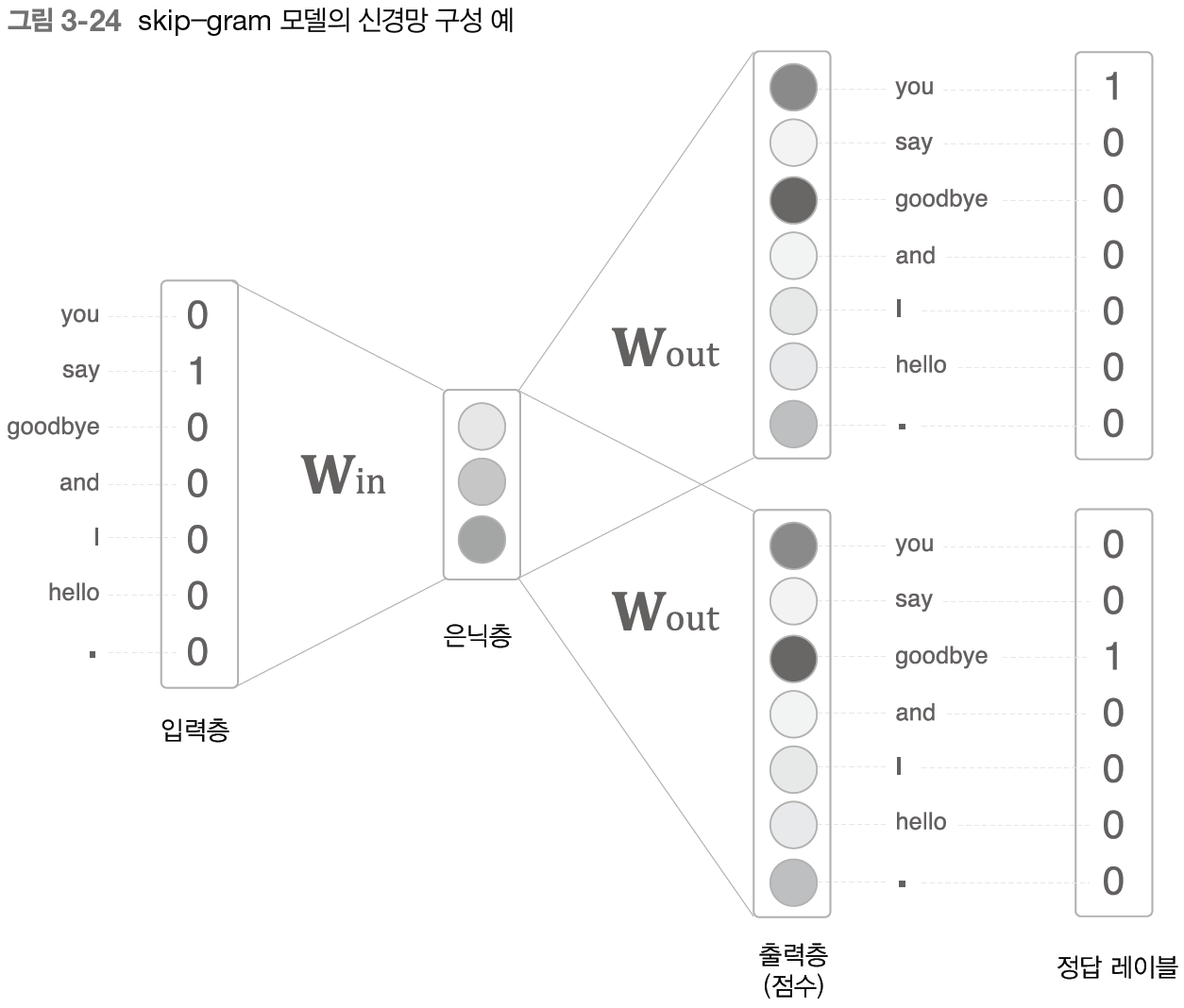
skip-gram 모델의 입력층은 하나이다. 한편 출력층은 맥락의 수만큼 존재한다. 따라서 각 출력층에서는 개별적으로 손실을 구하고, 이 개별 손실들을 모두 더한 값을 최종 손실로 한다.

skip-gram 모델의 확률을 나타내면 다음과 같다.

\[P(w_{t-1},w_{t+1}|w_{t})\]

맥락의 단어들 사이에 조건부 독립을 가정하고 다음과 같이 분해하고 이를 이용해 손실 함수를 유도할 수 있다.

\[P(w_{t-1},w_{t+1}|w_{t})=P(w_{t-1}|w_{t})P(w_{t+1}|w_{t})\] \[\begin{aligned} L&=-\log{P(w_{t-1},w_{t+1}|w_{t})}\\ &=-\log{P(w_{t-1}|w_{t})P(w_{t+1}|w_{t})}\\ &=-(\log{P(w_{t-1}|w_{t})} + \log{P(w_{t+1}|w_{t})}) \end{aligned}\]

이를 말뭉치 전체로 확장하면 다음과 같은 수식이 된다.

\[L=-\frac{1}{T}\sum^T_{t-1}(\log{P(w_{t-1}|w_{t})} + \log{P(w_{t+1}|w_{t})})\]

단어 분산 표현의 정밀도 면에서 skip-gram 모델의 결과가 CBOW 모델의 결과보다 더 좋은 경우가 많다. 특히 말뭉치가 커질수록 저빈도 단어나 유추 문제의 성능 면에서 skip-gram 모델이 더 뛰어난 경향이 있다. 반면, 학습 속도 면에선 CBOW 모델이 더 빠르다. skip-gram 모델은 손실을 맥락의 수만큼 구해서 계산해야하기 때문.