Coursera Deep Learning Logistic Regression with Neural Network

7 minute read

Coursera에서 Andrew Ng의 Neural Networks and Deep Learning을 수강하고 있다.
2주차 마지막에 Logistic Regression과 Neural Network를 이용하여 주어진 사진들이 고양이인지 아닌지를 분류하는 신경망을 구현하는 과제가 있다.

Welcome to the first (required) programming exercise of the deep learning specialization. In this notebook you will build your first image recognition algorithm. You will build a cat classifier that recognizes cats with 70% accuracy!

강좌에서 제공하는 Jupyter Notebook 파일을 차근차근 따라가면 약 70%의 정확성을 가지는 멋진 신경망을 구현할 수 있다.

1 - 로지스틱 회귀분석과 신경망을 이용하여 고양이 사진 분류하기

1.1 - Package

먼저 데이터 전처리, 로지스틱 회귀분석, 신경망 제작을 위해 필요한 패키지들을 임포트한다.

#Import packages
import numpy as np
import matplotlib.pyplot as plt
import h5py
import scipy
from PIL import Image
from scipy import ndimage
from lr_utils import load_dataset

%matplotlib inline

h5py 패키지는 HDF5 바이너리 데이터 포맷을 사용하기 위한 인터페이스 패키지이다.
lr_utils 패키지는 신경망 학습을 위한 고양이 사진 데이터셋이 들어있는 패키지이다.

1.2 - 데이터셋 준비

1.2.1 - 개요

("data.h5") 데이터셋이 주어진다. 이 데이터셋은 다음을 포함하고 있다.

train : 고양이(y=1) 또는 고양이가 아님(y=0) 라벨을 가지고 있는 이미지 트레이닝셋이다.
test : 고양이 또는 고양이가 아님 라벨을 가지고 있는 이미지 테스트셋이다.
각 이미지의 사이즈는 (num_px, num_px, 3) 이며 3은 이미지의 채널 수(RGB)를 의미한다.
각 이미지는 height = num_px, width = num_px 이다. 따라서, 각 이미지는 정사각형이다.

1.2.2 - 데이터 불러오기

이제 lr_utils에서 임포트한 함수를 통해 데이터셋을 불러온다.

# Loading the data (cat/non-cat)
train_set_x_orig, train_set_y, test_set_x_orig, test_set_y, classes = load_dataset()

load_dataset() 함수를 이용하여 각 변수에 데이터셋을 저장한다.

train_set_x_orig : 신경망을 트레이닝할 데이터셋 이미지들의 픽셀값들을 담은 행렬이다.
train_set_y : 신경망을 트레이닝할 데이터셋 이미지들의 라벨 값들을 담은 행렬이다.
test_set_x_orig : 신경망을 테스트할 데이터셋 이미지들의 픽셀값들을 담은 행렬이다.
test_set_y : 신경망을 테스트할 데이터셋 이미지들의 라벨 값들을 담은 행렬이다.
classes : 라벨 값들의 이름(cat / non-cat)이 있는 array이다.

위 변수들은 모두 numpy.ndarray 이며, ndarray 는 동일 타입의 원소가 담긴 다차원 행렬로 벡터 연산이 가능하다.

train_set_x_orig 과 test_set_x_orig 뒤에 _orig 가 붙어있는 이유는 이미지 데이터셋을 가공한 후 원본 데이터셋과 구분을 하기 위해 붙어있다.

1.2.3 - 이미지 출력하기

다음 코드를 통해 트레이닝 데이터셋의 이미지 파일 하나를 출력할 수 있다. index 값을 수정하면 다른 이미지 파일도 불러올 수 있다.

# Example of a picture
index = 2
plt.imshow(train_set_x_orig[index])
print ("y = " + str(train_set_y[:, index]) + ", it's a '" + classes[np.squeeze(train_set_y[:, index])].decode("utf-8") +  "' picture.")

Logistic_Regression_image1

1.2.4 - 이미지 갯수와 크기 확인하기

먼저, 불러온 데이터셋의 크기를 확인한다. numpy.ndarray 의 크기는 .shape 를 이용하여 확인할 수 있다.

print ("train_set_x_orig shape: " + str(train_set_x_orig.shape))
print ("train_set_y shape: " + str(train_set_y.shape))
print ("test_set_x_orig shape: " + str(test_set_x_orig.shape))
print ("test_set_y shape: " + str(test_set_y.shape))

# train_set_x_orig shape: (209, 64, 64, 3)
# train_set_y shape: (1, 209)
# test_set_x_orig shape: (50, 64, 64, 3)
# test_set_y shape: (1, 50)

train_set_x_orig 과 test_set_x_orig 의 shape 는 (m_train or m_test, num_px, num_px, channel) 이다.
train_set_y 와 test_set_y 의 shape 는 (label, m_train or m_test) 이다.
m_train or m_test 는 각 데이터셋의 이미지 갯수이다.

따라서 트레이닝셋의 이미지 갯수는 209개, 테스트셋의 이미지 갯수는 50개, 각 이미지의 크기(픽셀 수)는 64*64 임을 알 수 있다.

1.2.5 - 이미지 가공하기

현재 이미지의 형태는 (num_px, num_px, 3) 이기 때문에 다루기가 까다롭다. 신경망을 학습할 때 이미지를 다루기 쉽도록 (num_px * num_px * 3, m_train or m_test) 형태인 2차원 행렬로 바꿔준다.

# Reshape the training and test examples
train_set_x_flatten = train_set_x_orig.reshape(train_set_x_orig.shape[0], -1).T
test_set_x_flatten = test_set_x_orig.reshape(test_set_x_orig.shape[0], -1).T

print ("train_set_x_flatten shape: " + str(train_set_x_flatten.shape))
print ("test_set_x_flatten shape: " + str(test_set_x_flatten.shape))

# train_set_x_flatten shape: (12288, 209)
# test_set_x_flatten shape: (12288, 50)

.reshape(행의 수, 열의 수) : 행렬의 구조를 변환한다. 행의 수를 지정하고 열의 수에 -1 을 지정해주면 변환될 행렬의 열의 수는 알아서 지정해준다.
.T : 행렬을 전치(Transpose)한다. 전치행렬은 행과 열을 교환하여 얻는 행렬이다. 자세한 내용은 여기를 참고.

컬러 이미지를 나타내려면 각 픽셀에 대해 빨간색, 녹색, 파란색 채널(RGB)을 지정해야 하므로 픽셀 값은 실제로 0부터 255까지의 3개의 정수 벡터이다. 보통 데이터를 가공할 때 표준화 또는 정규화 하는 과정을 거쳐야 하지만 이미지 데이터셋은 행렬의 모든 값을 255(픽셀 채널의 최대값)로 나누는 것이 더 간단하고 잘 작동한다.

train_set_x = train_set_x_flatten/255.
test_set_x = test_set_x_flatten/255.

1.3 학습 알고리즘 구조

다음은 신경망이 이미지를 분류하는 과정을 나타낸 그림이다.

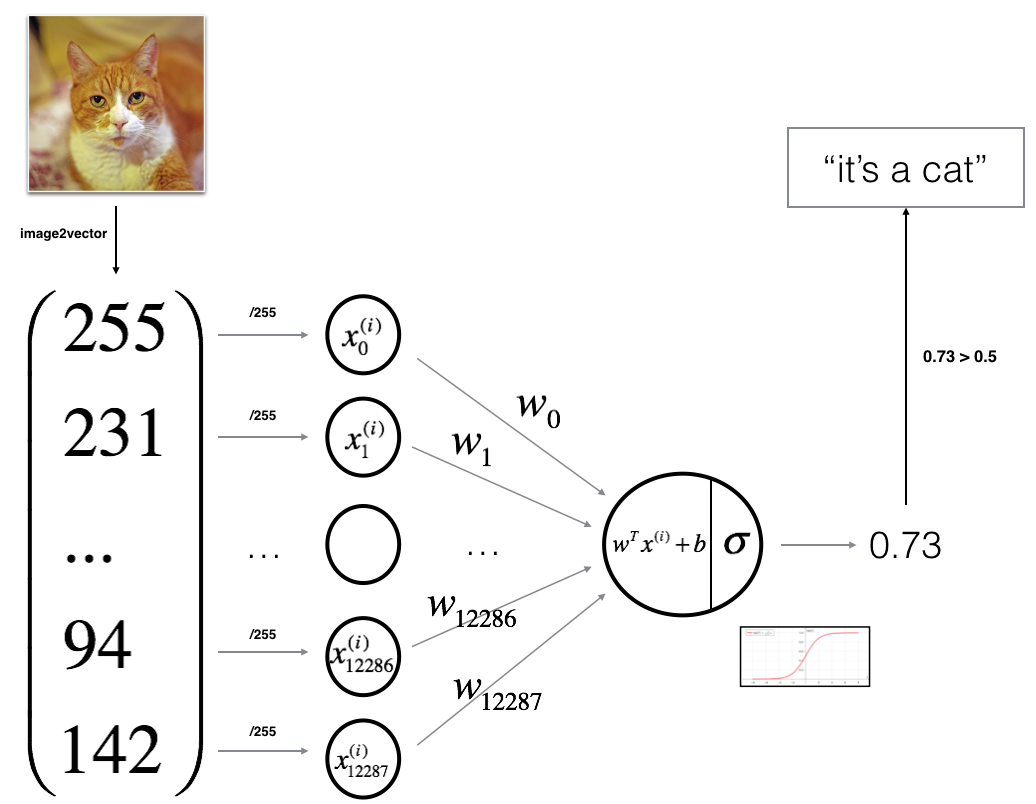
Logistic_Regression_image2

알고리즘의 수학적 표현을 살펴보자.

\[z^{(i)}=w^Tx^{(i)}+b\tag{1}\] \[\hat{y}^{(i)}=a^{(i)}=sigmoid(z^{(i)})\tag{2}\] \[\mathcal{L}(a^{(i)},y^{(i)})=-y^{(i)}log(a^{(i)})-(1-y^{(i)})log(1-a^{(i)})\tag{3}\] \[J=\frac{1}{m}\sum_{i=1}^m\mathcal{L}(a^{(i)},y^{(i)})\tag{4}\]

(i) 는 Layer의 index이다.
z 는 가중치(weight)의 전치행렬과 x행렬 을 내적(dot product)한 후 편향(bias) 을 더한 스칼라 값이다.
a 는 z 에 활성화 함수(sigmoid function) 를 적용하여 나온 이미지에 대한 라벨 예측 값(확률)이다.
$\mathcal{L}(a^{(i)},y^{(i)})$ 는 로지스틱 회귀의 비용(오차)함수이다.
J 는 전체 m에 대한 총 비용(오차)의 평균값이다.

이제 다음 스텝을 따라 신경망을 제작한다.

신경망 구조를 정의한다.
신경망의 각종 파라미터값(weight, bias)을 초기화 한다.
비용(오차)을 최소화하는 파라미터값을 구할 수 있도록 신경망을 학습시킨다.
학습된 신경망을 통해 테스트셋을 예측한다.
결과를 분석하고 결론을 내린다.

1.4 - 알고리즘 구현하기

1.4.1 - 활성화 함수 구현

위 그림과 수식을 통해 보았듯이 활성화 함수를 이용하여 라벨 예측 값을 구해야 한다. 다양한 활성화 함수가 있으며 상황에 따라 적절한 함수를 사용하면 된다.

\[sigmoid(x), tanh(x), ReLU(x), Leakly ReLU(x), softmax(x), ETC...\]

여기에선 시그모이드 함수를 활성화 함수로 구현하였다. 시그모이드 함수의 공식은 아래와 같다.

\[sigmoid(w^TX+b)=\frac{1}{1+e^{-(w^TX+b)}}\]

자연지수함수 $exp(x)$ 는 np.exp() 를 사용한다.

def sigmoid(z):
  s = 1/(1+np.exp(-z))

  return s

1.4.2 - 파라미터값 초기화 함수 구현

초기 파라미터값을 0 으로 초기화하기 위한 함수를 구현한다. 이 때, 가중치들은 벡터로 표현되어 있기 때문에 np.zeros() 함수를 이용하여 초기화 한다.

def initialize_with_zeros(dim):
  w = np.zeros(dim, 1)
  b = 0

  return w, b

이미지를 input(dim) 으로 넣는다면, w 의 shape 는 (num_px * num_px * 3, 1) 이 될 것 이다.

1.4.3 - 순전파와 역전파 구현

파라미터값을 초기화 하였으니 순전파와 역전파를 구현한다.

순전파
- 활성화 함수 값을 이용하여 비용함수를 계산한다. 공식은 아래와 같다.
\[A=sigmoid(w^TX+b)=(a^{(1)}, a^{(2)},..., a^{(m-1)}, a^{(m)})\tag{1}\] \[COST=J=-\frac{1}{m}\sum_{i=1}^my^{(i)}log(a^{(i)})+(1-y^{(i)})log(1-a^{(i)})\tag{2}\]
역전파
- 비용함수를 가중치 와 편향 으로 미분한 값을 계산한다. 공식은 아래와 같다.
\[\frac{\partial J}{\partial w} = \frac{1}{m}X(A-Y)^T\tag{1}\] \[\frac{\partial J}{\partial b} = \frac{1}{m} \sum_{i=1}^m (a^{(i)}-y^{(i)})\tag{2}\]

def propagate(w, b, X, Y):
  m = X.shape[1]

  # Forward propagation(From X To COST)
  A = sigmoid(np.dot(w.T, x) + b)
  cost = (-1/m)*np.sum(Y*np.log(A)+(1-Y)*np.log(1-A))

  # Backward propagation(To find grad)
  dw = (1/m)*np.dot(X, (A-Y).T)
  db = (1/m)*np.sum(A-Y)

  cost = np.squeeze(cost)

  grads = {"dw" : dw,
          "db" : db}

  return grads, cost

1.4.4 - 파라미터값 업데이트 함수 구현

비용함수를 계산하고 그에 대한 미분값을 구하는 함수를 구현했으니 이제 경사하강법을 사용하여 파라미터값을 업데이트하는 함수를 구현한다. 비용함수를 최소화하는 파라미터값을 찾는 것이 우리의 목표이다. 파라미터 $\theta$ 를 업데이트 할 때, 아래와 같은 공식을 사용한다.

\[\theta=\theta-\alpha d\theta\]

이 때, $\alpha$ 는 학습률(learning rate) 이며 1 이하의 값 을 가진다.

def optimize(w, b, X, Y, num_iterations, learning_rate, print_cost = False):
  costs = []

  for i in range(num_iterations):
    # Cost and gradient calculation
    grads, cost = propagate(w, b, X, Y)

    # Retrieve derivatives from grads
    dw = grads[dw]
    db = grads[db]

    # Update parameters
    w = w - learning_rate * dw
    b = b - learning_rate * db

    # Record the costs
    if i % 100 == 0:
      costs.append(cost)

    # Print the cost every 100 training iterations
    if print_cost and i % 100 == 0:
      print(f"Cost after iterations {i} : {cost}")

  params = {"w" : w,
            "b" : b}

  grads = {"dw" : dw,
           "db" : db}

  return params, grads, costs

1.4.5 - 예측 함수 구현

앞서 구현한 함수들을 이용하여 파라미터값 업데이트가 끝나면 아래의 두 단계를 거쳐 테스트셋을 가지고 결과를 예측할 수 있다.

Y 예측값(활성화 함수 값) 을 구한다. $(\hat{Y}=A=sigmoid(w^TX+b))$
Y 예측값을 0(if A <= 0.5) 또는 1(if A > 0.5) 로 변환한다.

def predict(w, b, X):
  m = X.shape[1]
  Y_prediction = np.zeros((1, m))
  w = w.reshape(X.shape[0], 1)

  # Compute vector "A" predicting the probabilities of a cat being present
  A = sigmoid(np.dot(w.T, X) + b)

  for i in range(A.shape[1]):    
    # Convert probabilities A[0,i] to actual predictions p[0,i]
    if A[0, i] <= 0.5:
      Y_prediction[0, i] = 0
    else:
      Y_prediction[0, i] = 1

    return Y_prediction

1.5 - 모든 함수를 합쳐 모델 구현하기

이제 고양이 사진을 분류하기 위한 모든 함수 구현이 마무리 되었다. 이제 앞서 구현한 모든 함수들을 하나로 합쳐 모델을 구현한다.

def model(X_train, Y_train, X_test, Y_test, num_iterations=2000, learning_rate=0.5, print_cost=False):
  # Initialize parameters with zeros
  w, b = initialize_with_zeros(X_train.shape[0])

  # Gradient  descent
  parameters, grads, costs = optimize(w, b, X_train, Y_train, num_iterations, learning_rate, print_cost)

  # Retrieve parameters w and b from dictionary "parameters"
  w = parameters["w"]
  b = parameters["b"]

  # Predict test/train set examples
  Y_prediction_test = predict(w, b, X_test)
  Y_prediction_train = predict(w, b, X_train)

  # Print train/test Errors
  print(f"train accuracy: {100 - np.mean(np.abs(Y_prediction_train - Y_train)) * 100}")
  print(f"test accuracy: {100 - np.mean(np.abs(Y_prediction_test - Y_test)) * 100}")

  d = {"costs" : costs,
       "Y_prediction_test" : Y_prediction_test,
       "Y_prediction_train" : Y_prediction_train,
       "w" : w,
       "b" : b,
       "learning_rate" : learning_rate,
       "num_iterations" : num_iterations}

  return d

d = model(train_set_x, train_set_y, test_set_x, test_set_y, num_iterations = 2000, learning_rate = 0.005, print_cost = True)

#Cost after iteration 0: 0.693147
#Cost after iteration 100: 0.584508
#Cost after iteration 200: 0.466949
#Cost after iteration 300: 0.376007
#Cost after iteration 400: 0.331463
#Cost after iteration 500: 0.303273
#Cost after iteration 600: 0.279880
#Cost after iteration 700: 0.260042
#Cost after iteration 800: 0.242941
#Cost after iteration 900: 0.228004
#Cost after iteration 1000: 0.214820
#Cost after iteration 1100: 0.203078
#Cost after iteration 1200: 0.192544
#Cost after iteration 1300: 0.183033
#Cost after iteration 1400: 0.174399
#Cost after iteration 1500: 0.166521
#Cost after iteration 1600: 0.159305
#Cost after iteration 1700: 0.152667
#Cost after iteration 1800: 0.146542
#Cost after iteration 1900: 0.140872
#train accuracy: 99.04306220095694 %
#test accuracy: 70.0 %

트레이닝셋의 정확도는 거의 100%에 이르지만 테스트셋의 정확도는 70%이다. 적은 데이터셋과 로지스틱 회귀가 선형 분류임을 감안할 때 나쁘지 않은 분류 모델이라고 생각한다. 다만, 분류 모델이 트레이닝셋에 과적합(overfitting) 되었음을 알 수 있다.

Share on

Twitter Facebook LinkedIn

Mintflavor